画像をダウンロード sin 2x tan 2x formula 640832

Learn how to solve trigonometric identities problems step by step online Prove the trigonometric identity sin(2x)tan(x)=tan(x)cos(2x) Applying the tangent identityAprende en línea a resolver problemas de identidades trigonométricas paso a paso Demostrar la identidad trigonométrica tan(x)^2sin(x)^2=tan(x)^2sin(x)^2 Aplicamos la identidad trigonométrica \tan\left(x\right)^n=\frac{\sin\left(x\right)^n}{\cos\left(x\right)^n}, donde n=2 Combinar todos los términos en una única fracción con \cos\left(x\right)^2 como común denominadorThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the Formula

Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11

Sin 2x tan 2x formula

Sin 2x tan 2x formula-Practice Example for Sin 2x If we want to solve the following equation We will follow the following steps Step 1) Use the Double angle formula Sin 2x = 2 Sin x Cos x Step 2) Let's rearrange it and factorize 2Sinx Cosx – sinx = 0 Sin x(2 cos x 1) = 0 So, a) Sinx =0 or b) cos2x 1 = 0 Step 3) Let's consider Sin x = 0Get an answer for 'Prove tan^2x sin^2x = tan^2x sin^2x' and find homework help for other Math questions at eNotes

Packet 21 Trigonometric Identities Ppt Download

Tan2x Formula is also known as the double angle function of tangent Let's look into the double angle function of tangent ie, tan2x Formula is as shown below tan 2x = 2tan x / 1−tan2xDouble Angle Formulas ( ) ( ) ( ) 22 2 2 2 sin22sincos cos2cossin 2cos1 12sin 2tan tan2 1tan qqq qqq q q q q q = ====Degrees to Radians Formulas If x is an angle in degrees and t is an angle in radiansThere are two basic formulas for Sin 2x Sin (2x) = 2 sinx cosx, and Sin (2x) = 2tan (x)​/ (1 tan 2 (x))Sin 2x sin(2x) Identity for sin 2x Formula for sin 2x Prove That sin(2x)=2tanx/(1 tan^2x)#sin, #sine, #sine of 2x, #sin 2x, #trigonometry

You need to write sin 2x and cos 2x in terms of tanx such that `sin 2x = (2 tan x)/(1 tan^2 x);4 sin 2 x tan 2 x csc 2 x cot 2 x − 6 = 0 ( 2 sin x ) 2 csc 2 x − 2 ⋅ 2 sin x ⋅ csc x ( tan x ) 2 ( cot x ) 2 − 2 ⋅ tan x ⋅ cot x = 0 ( 2 sin x − csc x ) 2 ( tan x − cot x ) 2 = 0Solve for x cot(x)tan(x)=2/(sin(2x)) Simplify each term Tap for more steps Rewrite in terms of sines and cosines Rewrite in terms of sines and cosines Take the inverse cosine of both sides of the equation to extract from inside the cosine The complete solution is the set of all solutions

Solution for 12 and x terminates in 13 nd sin 2x, cos 2x, and tan 2x if sin x= sin 2x cos 2x %3D tan 2x %3D IITake the inverse cosine of both sides of the equation to extract from inside the cosine LH S = tan2x −sin2x = (tanx sinx)(tanx −sinx) = (sinx cosx sinx)(sinx cosx −sinx) = sin2x(1 cosx 1)(1 cosx −1) = sin2x(secx 1)(secx − 1)

Answered Power Reducing Formulas Cos 2x 1 Cos Bartleby

Tan 2x Formula What Is Tan 2x Formula Examples

1) Show that the equation tan 2x = 5 sinx 2x can be written in the form (15 cos 2x) sin 2x = 0 Here I just rearranged the first equation using sin 2x / cos 2x = 5 sin 2x 2) Hence solve for 0Sin(x y) cosxcosy Formule di duplicazione Formule di bisezione sin2x= 2sinxcosx sin x 2 = r 1 cosx 2 cos(2x) = cos2 x sin2 x= cos x 2 = r 1 cosx 2 = 2cos2 x 1 = 1 2sin2 x tan(2x) = 2tanx 1 tan2 x tan x 2 = r 1 cosx 1 cosx Formule di triplicazione = 1 cosx sinx = sin(3x) = 3sinx 4sin3 x = sinx 1 cosx cos(3x) = 4cos3 x 3cosx You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

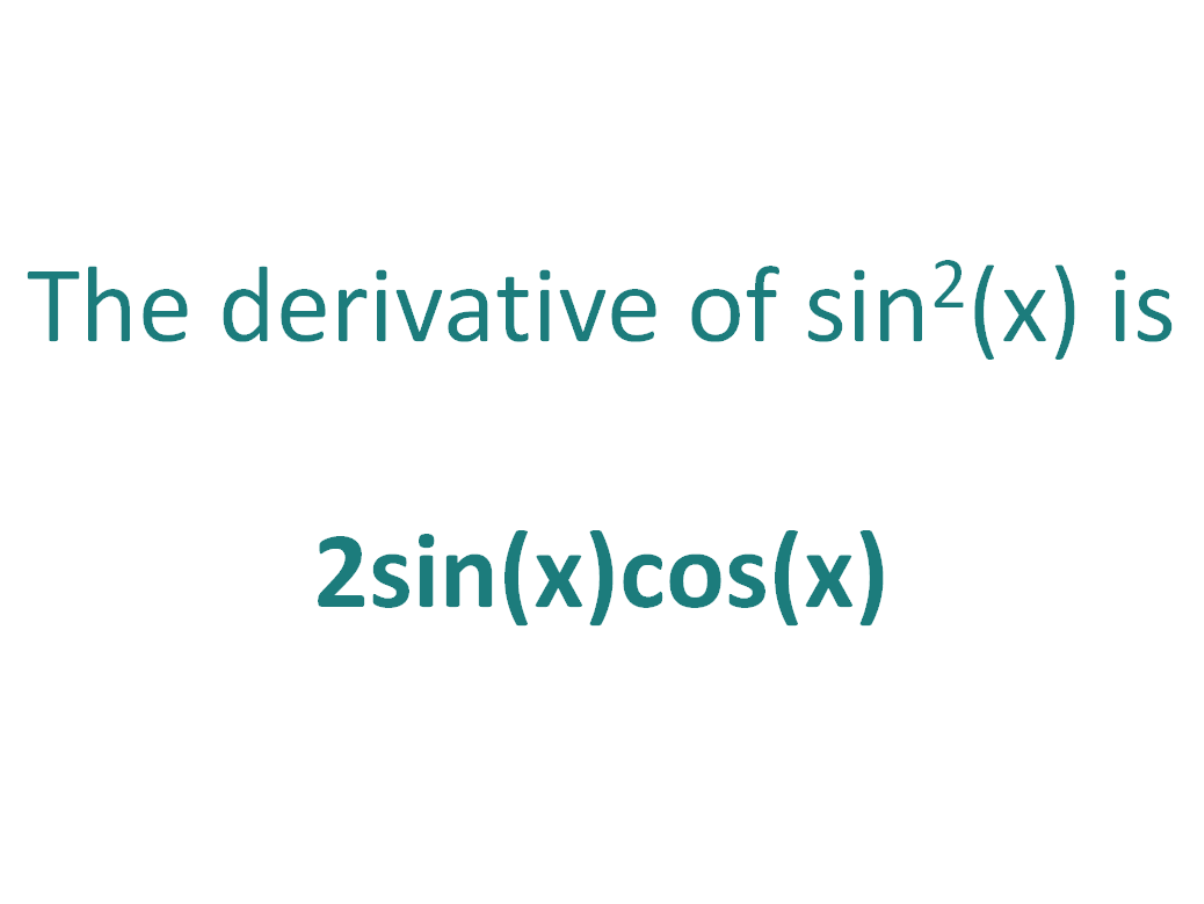
The Derivative Of Sin 2x Derivativeit

Learn how to solve trigonometric identities problems step by step online Prove the trigonometric identity tan(x)^2sin(x)^2=tan(x)^2sin(x)^2 Apply the trigonometric identity \tan\left(x\right)^n=\frac{\sin\left(x\right)^n}{\cos\left(x\right)^n}, where n=2 Combine all terms into a single fraction with \cos\left(x\right)^2 as common denominator In this article, you will learn how to use each double angle formula for sine, cosine, and tangent in simplifying and evaluating trigonometric functions and equations This article also includes double angle formulas proof and word problems For the exercises 58, find the exact values of a) sin(2x), b) cos(2x) and c) tan(2x) without solving for x 5) If sinx = 1 8 and x is in quadrant I Answer 3 √ 7 32 31 32 3 √ 7 31 6) If cosx = 2 3, and x is in quadrant I 7) If cosx = − 1 2, and x is in quadrant III Answer

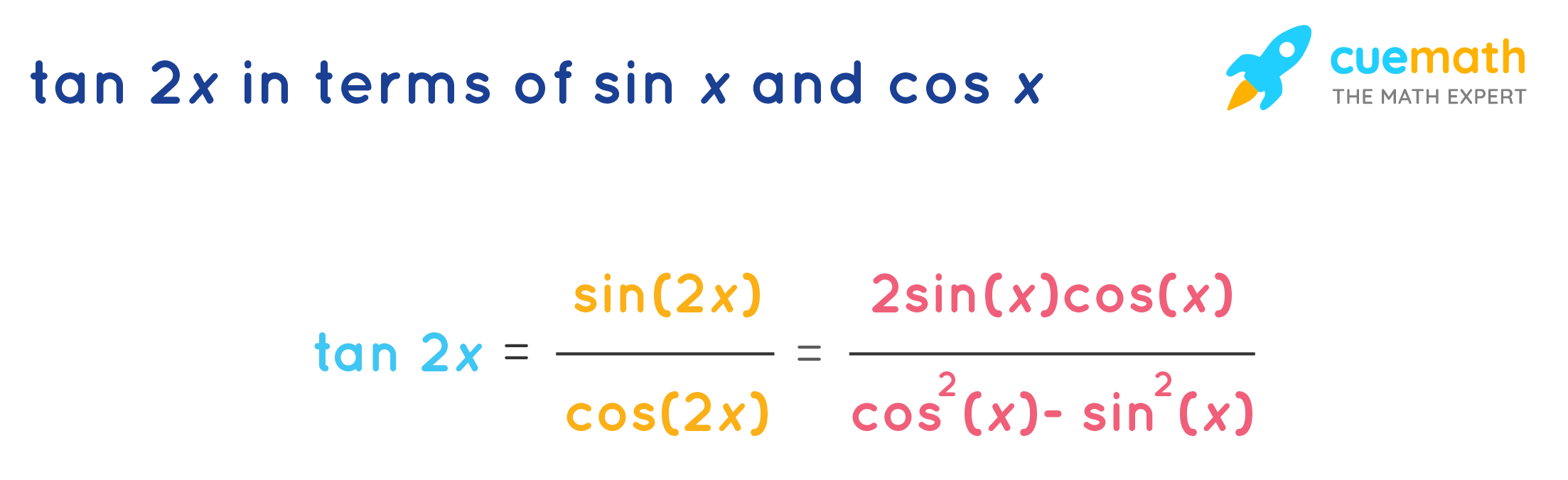
Tan 2x Formula What Is Tan 2x Formula Examples

Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube

Uit deze laatste formule volgt dan eenvoudig, wegens 1 2sin 2 p = 1 sin 2 p sin 2 p = cos 2 p sin 2 p cos 2p = cos 2 p sin 2 p Tweede methode We nemen een cirkel met middelpunt O en S = ½ AD OB = ½ sin(y) = ½ sin(180 2x)= ½ sin\sin \cos \tan \cot \csc \sec \alpha \beta \gamma \delta \zeta \eta \theta \iota \kappa \lambda \mu \nu \xi \pi \rho \sigma \tau To prove a trigonometric identity you have to show that one side of the equation can be transformedAnswered 2 years ago tan (x) is an odd function which is symmetric about its origin tan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x)

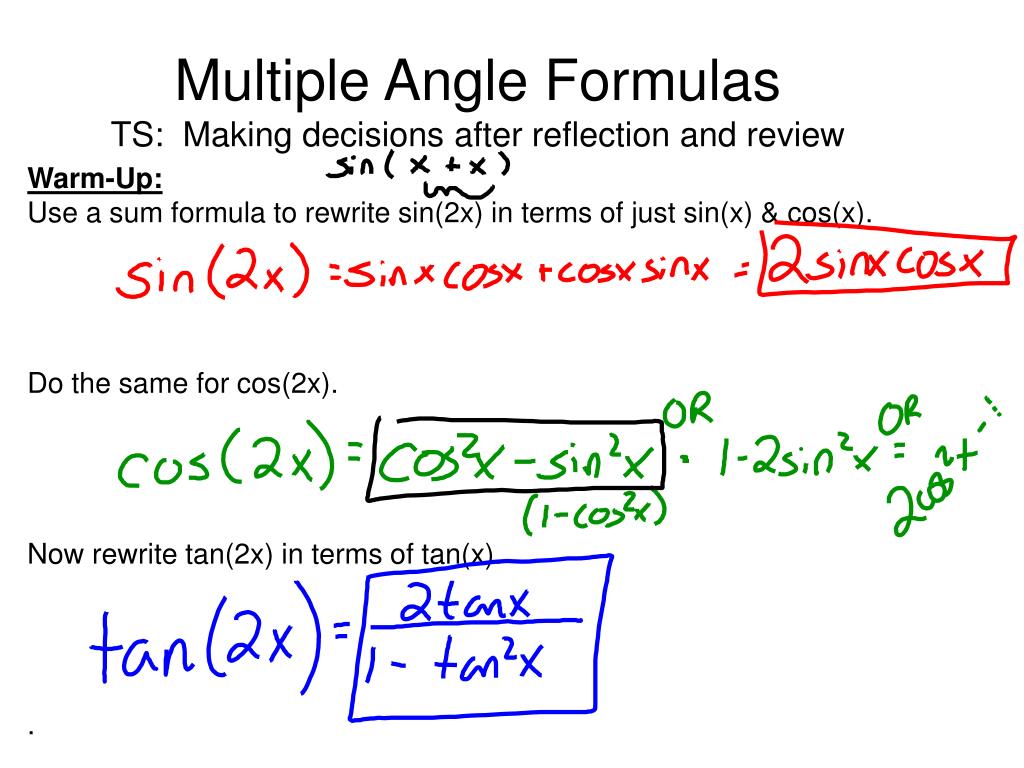
Lesson 4 5 Double Angle Formulas

Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id

Find an answer to your question verify formula texsin^2xtan^2xcos^2x =sec^2x/tex flowerwolf9 flowerwolf9 Mathematics Middle School answered Verify formula 1 See answer flowerwolf9 is waiting for your help Add yourCos 2x = (1tan^2 x)/(1 tan^2 x)` Plugging `tan x = sqrt6/3` in the formulas above yields `sinIdentity sin(2x) Identities Pythagorean;

Trigonometric Identities Trigonometric Functions Trigonometry

How Do You Solve 1 Tan 2x 6 2sec 2x Socratic

Since, the general solution of any trigonometric equation is given as sin x = sin y, implies x = nπ (– 1) n y, where n ∈ Z cos x = cos y, implies x = 2nπ ± y, where n ∈ Z tan x = tan y, implies x = nπ y, where n ∈ Z (i) Given as sin 2x = √3/2 Now, let us simplify, sin 2x = √3/2 = sin(π/3) ∴ the general solution is Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin ⁡ \sin sin andFor each of the three trigonometric substitutions above we will verify that we can ignore the absolute value in each case when encountering a radical 🔗 For x = asinθ, x = a sin ⁡ θ, the expression √a2 −x2 a 2 − x 2 becomes √a2−x2 = √a2−a2sin2θ= √a2(1−sin2θ)= a√cos2θ= acosθ = acosθ a 2 − x 2 = a 2 − a 2

B Suppose I Know That Sin X And X In Qiii Use Chegg Com

How To Prove The Identity In Tanx Cotx 2 Sin2x Quora

List of Trigonometric sin2x cos2x tan2x tan3x theta formula/identity Proof in terms of tanx, sin3x cos3x formula/identity, sin2xcos2x sin square x plus cos square x, cos sin a cos sin b sin cos a plus minus sin cos bIn mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many othersThe equation we want to solve is \sin(2x)\tan(x) You deduced correctly that we now have to solve 2\sin(x)\cos(x)\frac{\sin(x)}{\cos(x)}=0 which we can rewrite to 2

Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions

Find The General Solution For Each Of The Following Equations I Cos 4 X Cos 2x Ii Cos 3x Cos X Cos 2x 0 Iii Sin 2x

Tan^2⁡x sin^2⁡x cos^2x = (1 cos2x)/2 Simplify and write the trigonometric expression in terms of sine and cosine tan^2 xsec^2 x= The following equation expresses a relationship in terms of one variable However, you are asked to rewrite the equation in terms of a different variable3103 The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae,Sin ⁡ 2 x = tan ⁡ x (1 cos ⁡ 2 x) \sin 2x=\tan x (1\cos 2x) sin 2 x = tan x (1 cos 2 x) We have sin ⁡ x cos ⁡ x ( 1 cos ⁡ 2 x ) = sin ⁡ x cos ⁡ x ( 1 2 cos ⁡ 2 x − 1 ) = sin ⁡ x cos ⁡ x ( 2 cos ⁡ 2 x ) = 2 sin ⁡ x cos ⁡ x = sin ⁡ 2 xTan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x) Then, tan2x formula = sin (2x)/cos (2x) Tan 2x can also be written in terms of sin x and cos x, Tan2x Formula in terms of cos x = 2 s i n ( x) c o s ( x) c o s 2 x − s i n 2 x

Tan 2x Sin 2x Tan 2x Sin 2x

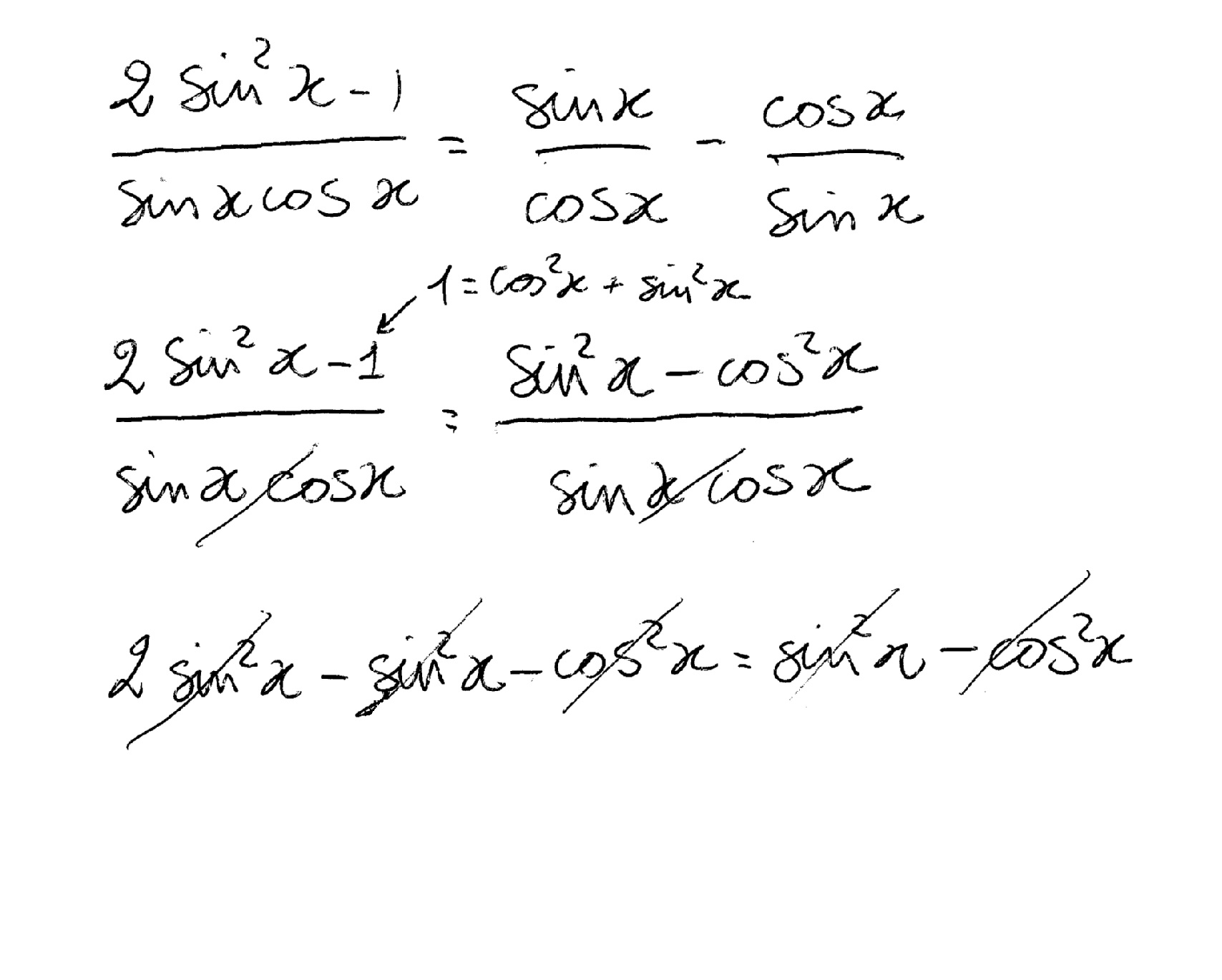
How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic

Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example Tan 2x formula in terms of sin xThree examples are that (1) any trigonometric expression can be converted to an expression in terms of only sin and cos, (2) expressions involving exp(x) can be converted to their hyperbolic forms, and (3) a trigonometric function with an argument of the form q ⁢Sine, tangent, cotangent, and cosecant are odd Answer ∫ cos 3 x sin 2 x d x = 1 3 sin 3 x − 1 5 sin 5 x C In the next example, we see the strategy that must be applied when there are only even powers of sinx and cosx For integrals of this type, the identities sin2x = 1 2 − 1 2cos(2x) = 1 − cos(2x) 2 and

Q Tbn And9gcswqgrwxfu3ry9lhuwrnhzq Lnjumaniii4kgzg4 Wagpp Cjba Usqp Cau

Examples Double Angle Formulas Ppt Download

Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be usedStack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Putting cos 2 x = 1 – sin 2 x cos 2x = cos 2 x – sin 2 x = 1 – sin 2 x – sin 2 x = 1 – 2sin 2 x Putting sin 2 x = 1 – cos 2 x cos 2x = cos 2 x – sin 2 x = cos 2 x – (1 – cos 2 x) = cos 2 x – 1 cos 2 x = 2cos 2 x – 1 For tan 2x

Problem 4 Using The Sin And Cos Addition Formulas Chegg Com

Sin2x Cos2x 1 Proof

Formula sin ⁡ 2 θ = 2 tan ⁡ θ 1 tan 2 ⁡ θ A trigonometric identity that expresses the expansion of sine of double angle function in terms of tan function is called the sine of double angle identity in tangent function  Use the fact that tanx = sinx cosx and sin2x = 2sinxcosx So 2 sinx cosx ⋅ 1 1 sinx cos2x = 2sinxcosx 2 sinx cosx ⋅ cos2x cos2x sin2x = 2sinxcosx 2 sinx cosx ⋅ cos2 x cos2x sin2x = 2sinxcosxDerivative Of sin^2x, sin^2(2x) – The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable Common trigonometric functions include sin(x), cos(x) and tan(x) For example, the derivative of f(x) = sin(x) is represented as f ′(a) = cos(a) f ′(a) is the rate of change

Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath

Sin2x Cos2x 1 Proof

Formulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angle double of the angle present in their formulas Sin 2x Formula Sin 2x formula is 2sinxcosx Image will be uploaded soon $$ \tan(x)\tan(3x)=2\sin(2x) $$ Thanks in advance!• Sine sin 2x = 2 sin x cos x • Cosine cos 2x = cos2 x – sin2 x = 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent

The Young Math Analysis 101 I D 3 Unit Q Pythagorean Identities

Example 14 Show Tan 3x Tan 2x Tan X Tan 3x Tan 2x Tan X

 Learn formula of tan(2x) or tan(2A) or tan(2θ) or tan(2α) identity with introduction and geometric proof to expand or simplify tan of double angleDividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes tan 2 (x)2 x Now let a = sin 2 x, write your equation in terms of a and b, and see what it tells you about a and b Since this is a homework, some intermediate steps are omitted and left for you to work out which you should be able to factor into 3 cases Solve each case for xCos(2x) = cos 2(x)−sin (x) sin(2x) = 2sin(x)cos(x) = 2cos2(x)−1 = 1−2sin2(x) tan(2x) = 2tan(x) 1−tan2(x) Formules du demiangle cos 2(x) = 1cos(2x) 2 sin (x) = 1−cos(2x) 2 tan(x) = sin(2x) 1cos(2x) = 1−cos(2x) sin(2x) En posant t = tan x 2 pour x 6≡π 2π, on a cos(x) = 1−t2 1t 2, sin(x) = 2t 1t et tan(x) = 2t 1−t

Prove That Tan 8x Tan 6x Tan 2x Tan 8x Tan 6x Tan 2x

Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh

 Free tangent line calculator find the equation of the tangent line given a point or the intercept stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyDec 27, 19 \(\cos 2X = \frac{\cos ^{2}X – \sin ^{2}X}{\cos ^{2}X \sin ^{2}X} Since, cos ^{2}X \sin ^{2}X = 1 \) Dividing both numerator and denominator by

2

Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11

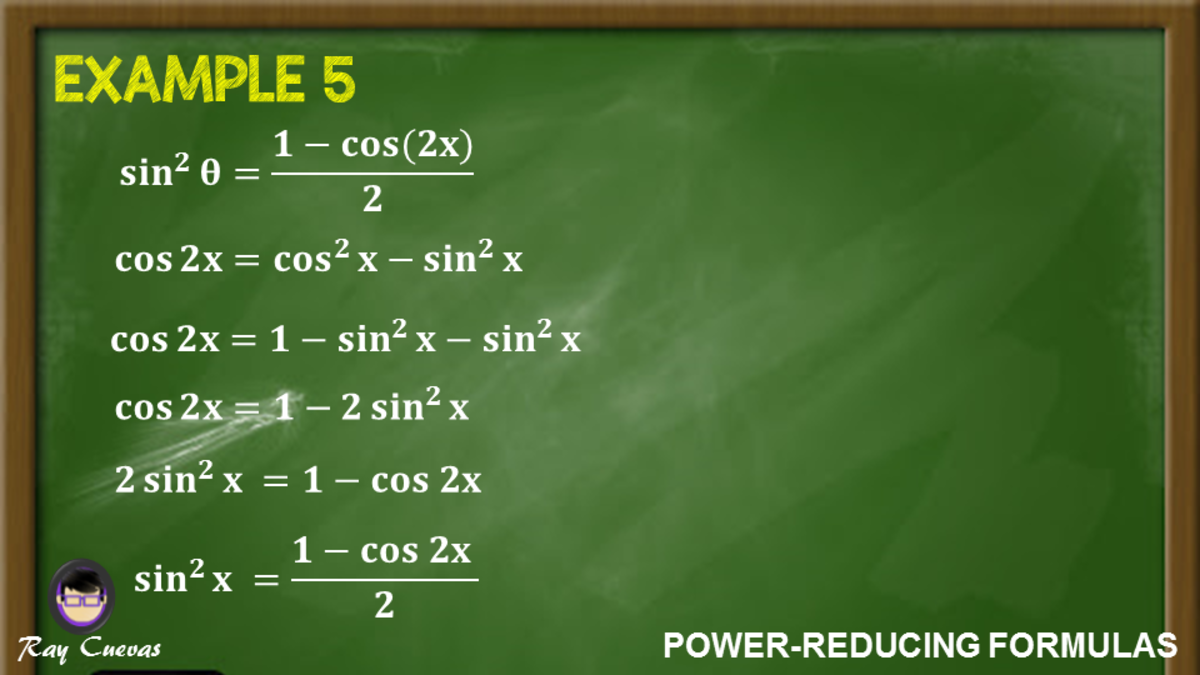
Power Reducing Formulas And How To Use Them With Examples Owlcation

Http Www Pstcc Edu Facstaff Jwlamb 1730 7 3 Pdf

If Sin2x N Sin 2y Then The Value Of Tan X Y Tan X Y Brainly In

Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube

Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In

Sin 2 X Identities Regan Cletus

Derivative Of Tan X Old Video Khan Academy

Cos X 1 Tan 2x Cos 2xsec X Gauthmath

Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3

Cos2x Sin2x Identity

Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube

Pdf Telecharger Cos 2x Sin 2x Gratuit Pdf Pdfprof Com

Www Jensenmath Ca Unit 5 pretest review solutions Pdf

Solved 10 Points Salgtrig4 7 Write The Given Expression As An Algebraic Expression In X Cos 2 Tan1m E Find The Exact Value Of The Given Course Hero

Sin2x Cos2x 1 Proof

Derivative Rules For Trigonometric Functions

Tan 2x 1 Sec 2x Tan X Sin X Cos X 2 1 Sin 2x Youtube

Formulas To Know Some Trig Identities Sin2x Cos 2x 1 Tan2x

Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube

1

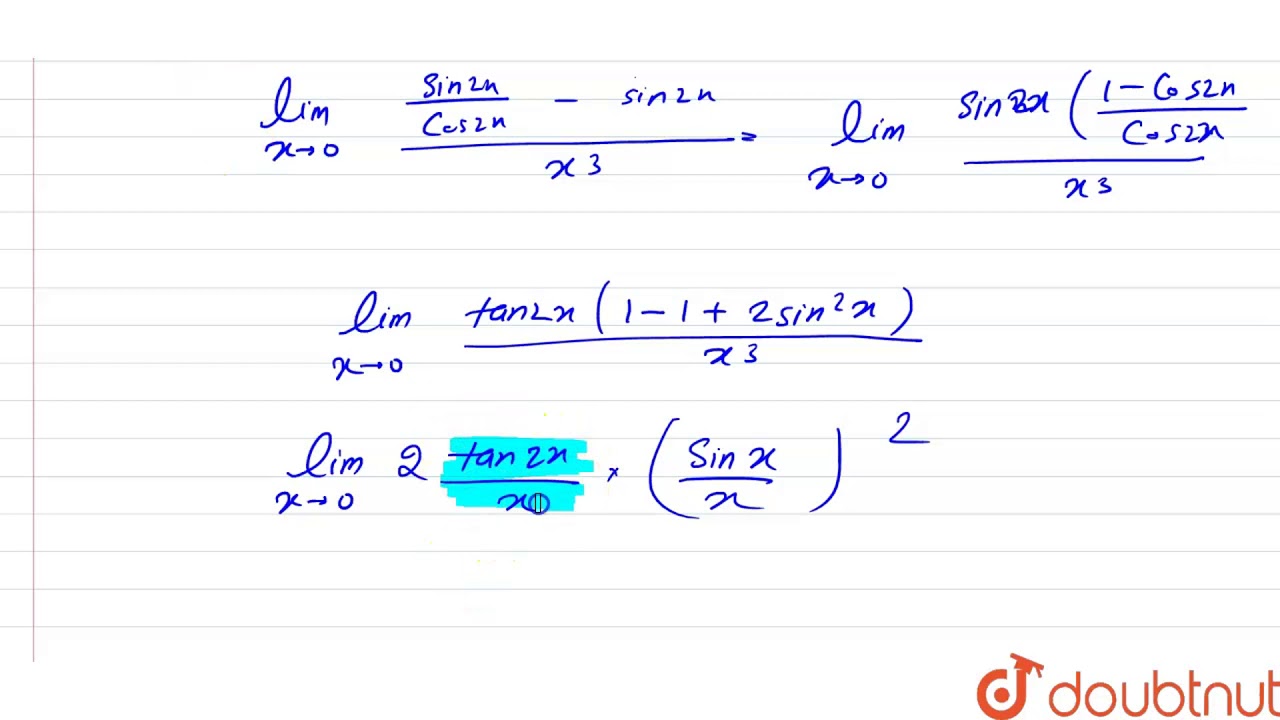
Evaluate The Following Limits Lim Xto0 Tan2x Sin2x X 3 Youtube

Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf

Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2

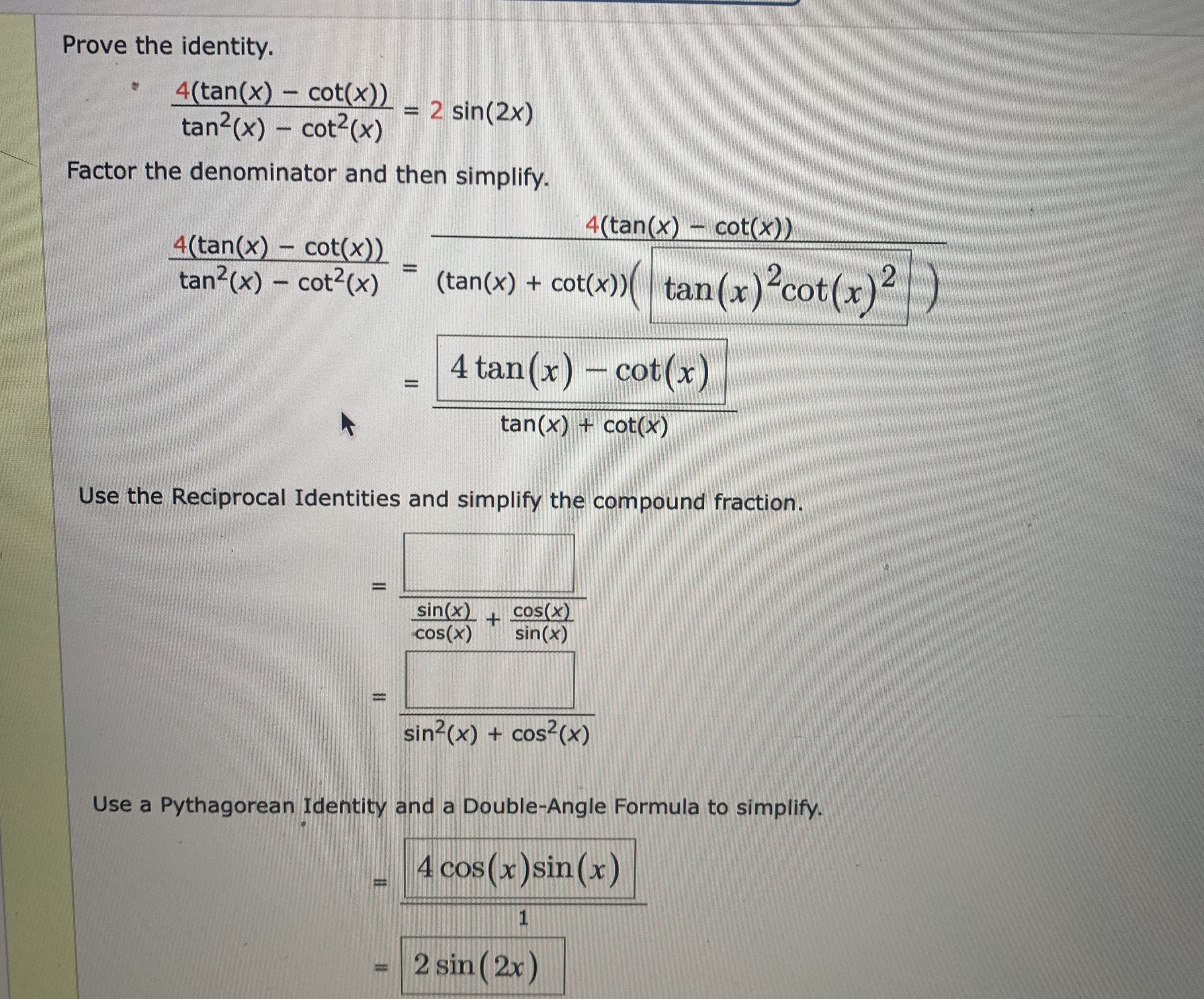
Answered Prove The Identity 4 Tan X Cot X Bartleby

Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id

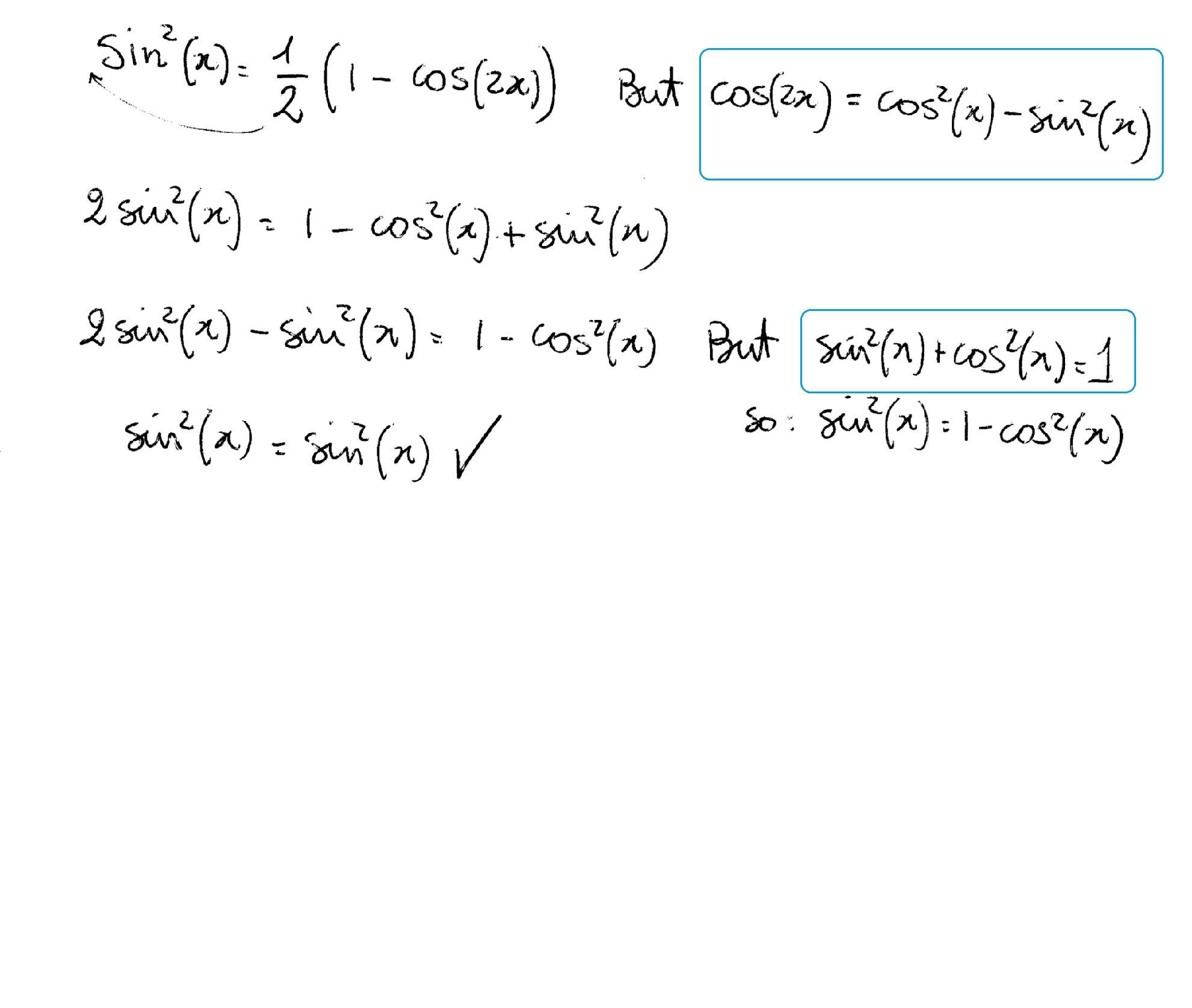
How Do You Verify Sin 2 X 1 2 1 Cos2x Socratic

Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh

Solve Tan X Tan 2x Sqrt 3 Tan X Tan 2x Sqrt 3

2

Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com

Packet 21 Trigonometric Identities Ppt Download

Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

3 Use Double Angle Formulas To Find The Exact Value Chegg Com

Let Tan 2x 1 2tan 2 Y Then Prove That Cos 2y 1 2cos 2x

Powers Of Trigonometric Functions

Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2

Let Lim X To 0 Sin 2x Tan X 2 L And Lim X To 0 E 2x 1 X L 2 Then The Value Of L 1 L 2 Is

Trigonometry Functions User S Blog

Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 11 Trigonometric Equations Download Free Pdf

1

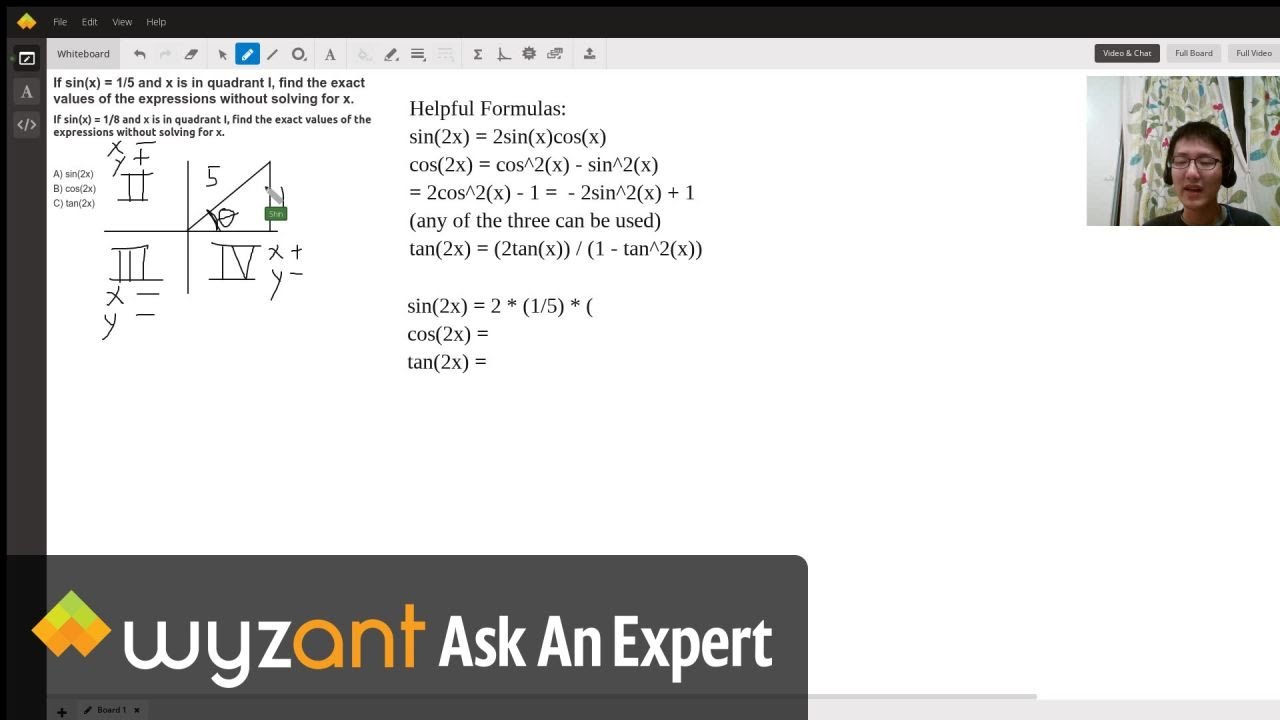
If Sin X 1 5 And X Is In Quadrant I Find The Exact Values Of The Expressions Without Solving For X Wyzant Ask An Expert

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

1

Mafiadoc Com Download Section 73 Double Angle Half Angle And Sum Product Identities 59d8ddd0fc79f562c Html

Double Angle Formulas What Are Double Angle Formulas Examples

Ppt Analytic Trig Powerpoint Presentation Free Download Id

Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Ppt Download

9 3 Other Identities Ppt Download

Http Www Mayfieldschools Org Downloads 4 8 double angle formulas key Pdf

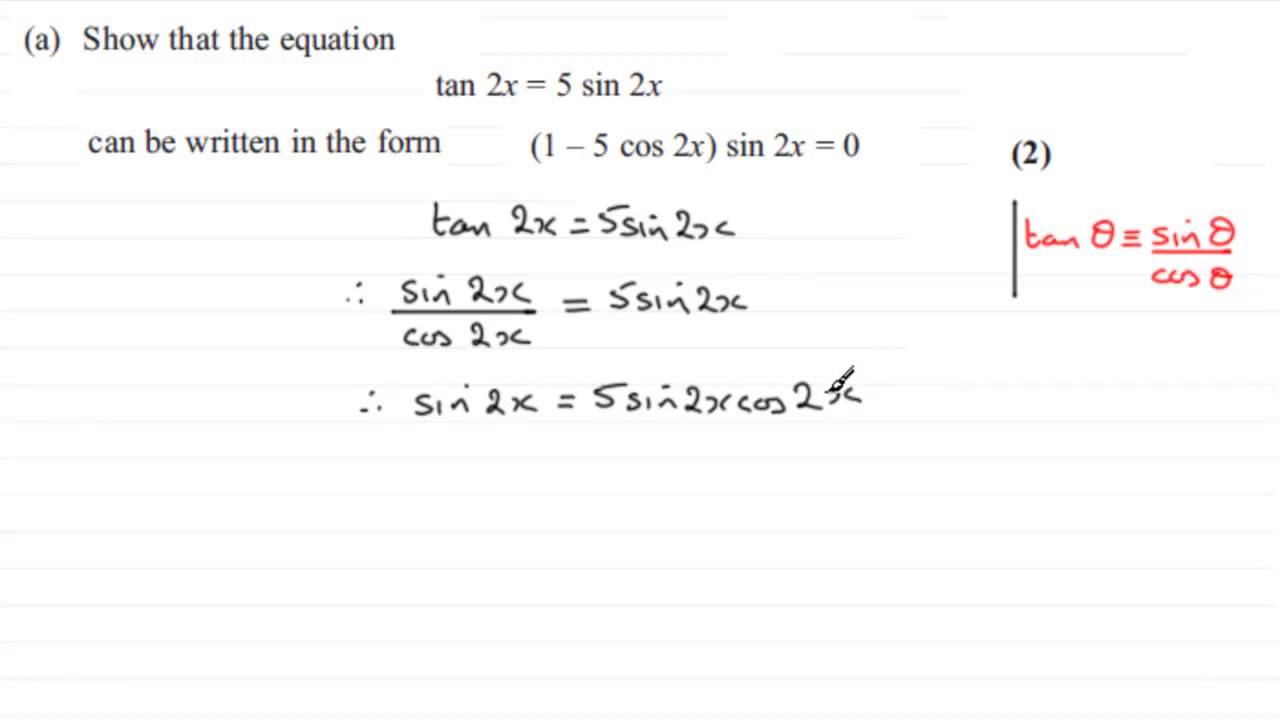
Edexcel Core Mathematics C2 June 12 Solutions Examples Worksheets Videos Activities

Integral 2 Sin X 18 Dx Rayeard

Trig Identities And Derivatives Notes Math 1b Docsity

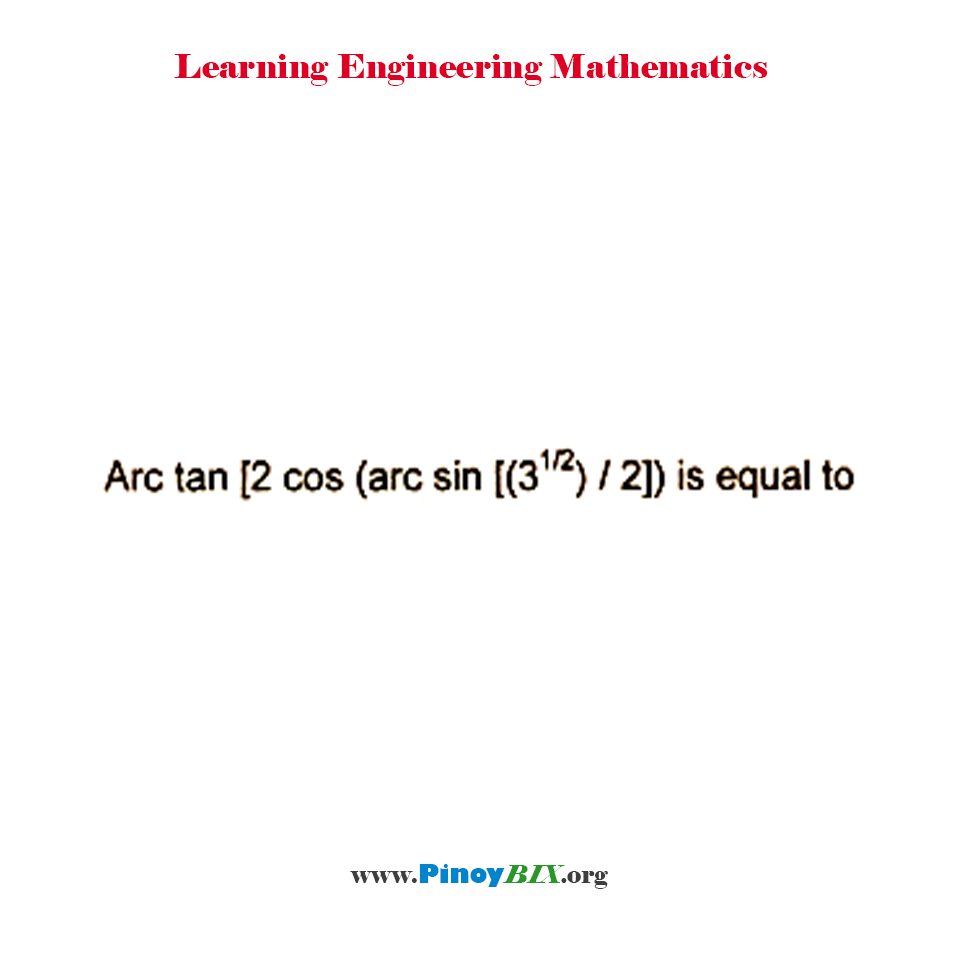
Solution Arc Tan 2cos Arc Sin 3 1 2 2 Is Equal To

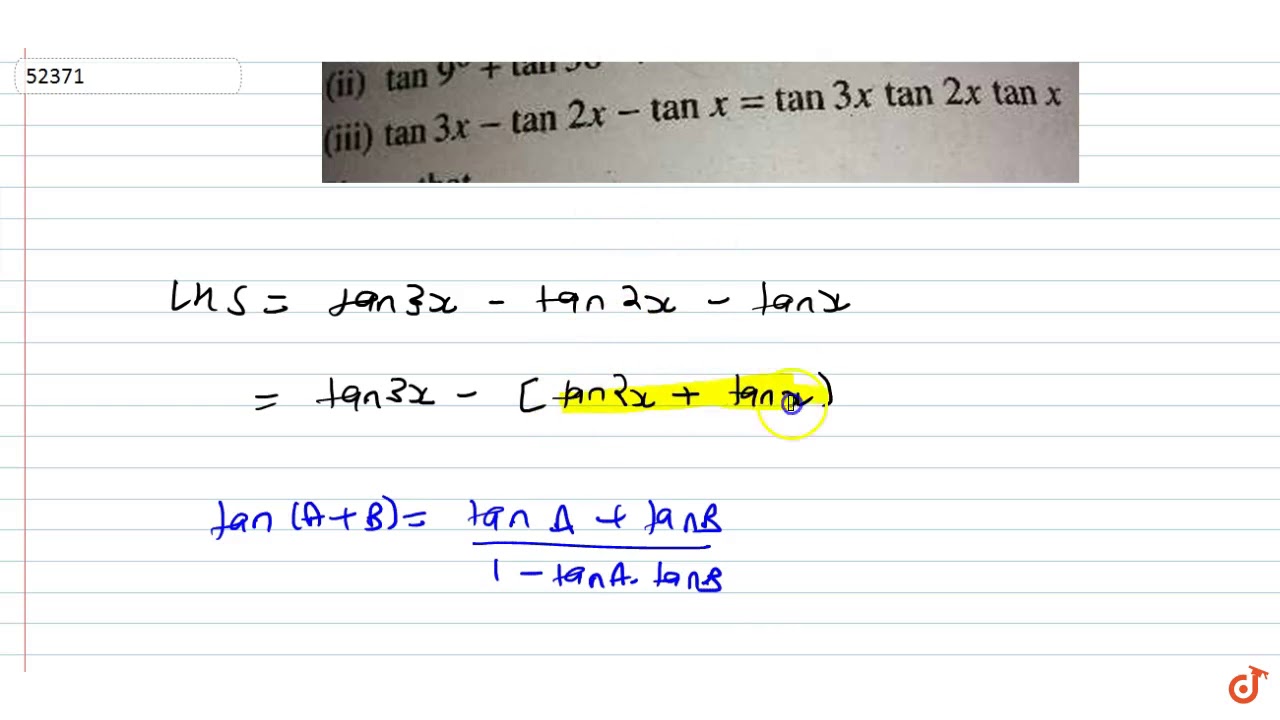
Tan 3x Tan 2x Tan X Tan 3x Tan 2x Tan X Youtube

The Value Of Lim X Pi 2 Tan 2x Sqrt 2sin 2x 3sinx 4 Sqrt Sin 2 X 6sinx 2 Is Equal To

Tan 2x 1 Sec 2x Tan X

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Find Sin2x Cos2x Andtan2xit Cosx 3 And X Terminat Gauthmath

Day 3 Hw 1 To 2 Find Sin2x Cos2x And Tan2x Given One Trig Value And The Quadrant Youtube

2

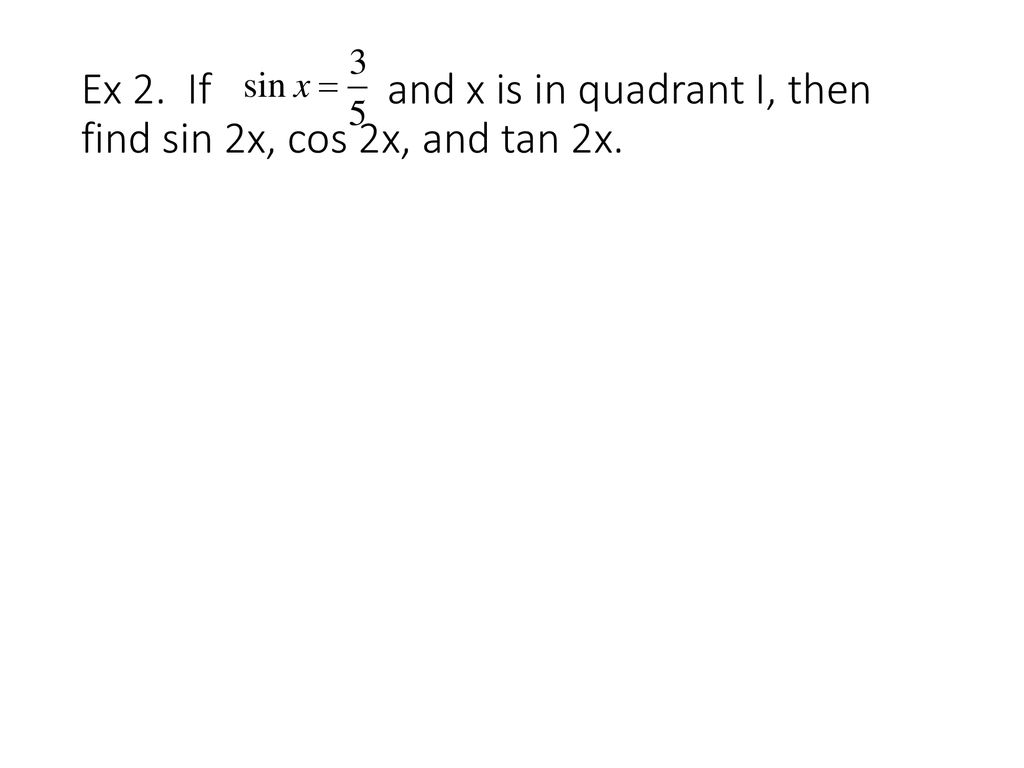
Double Angle Half Angle Formulas Ppt Download

Section 7 3 Double Angle Half Angle And Chegg Com

Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P

Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In

Integration Calculus Notes

Int Dx Sin 2x Tan 2x

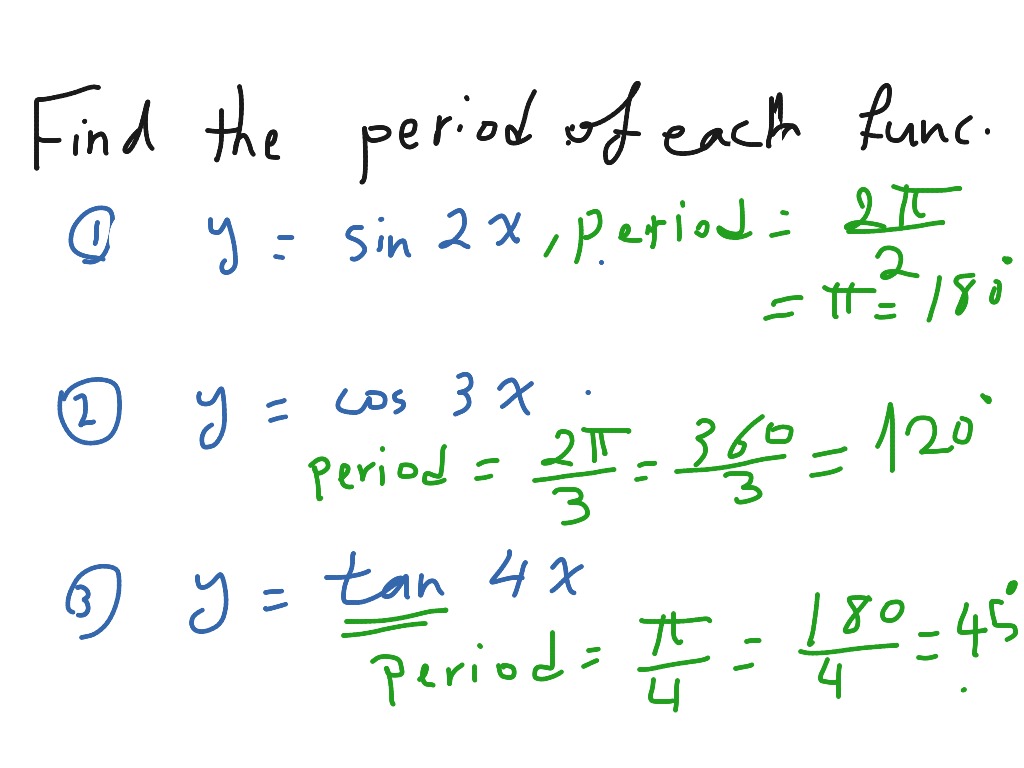
Find The Period Of Sin2x Cos 3x Tan 4 X Math Trigonometry Showme

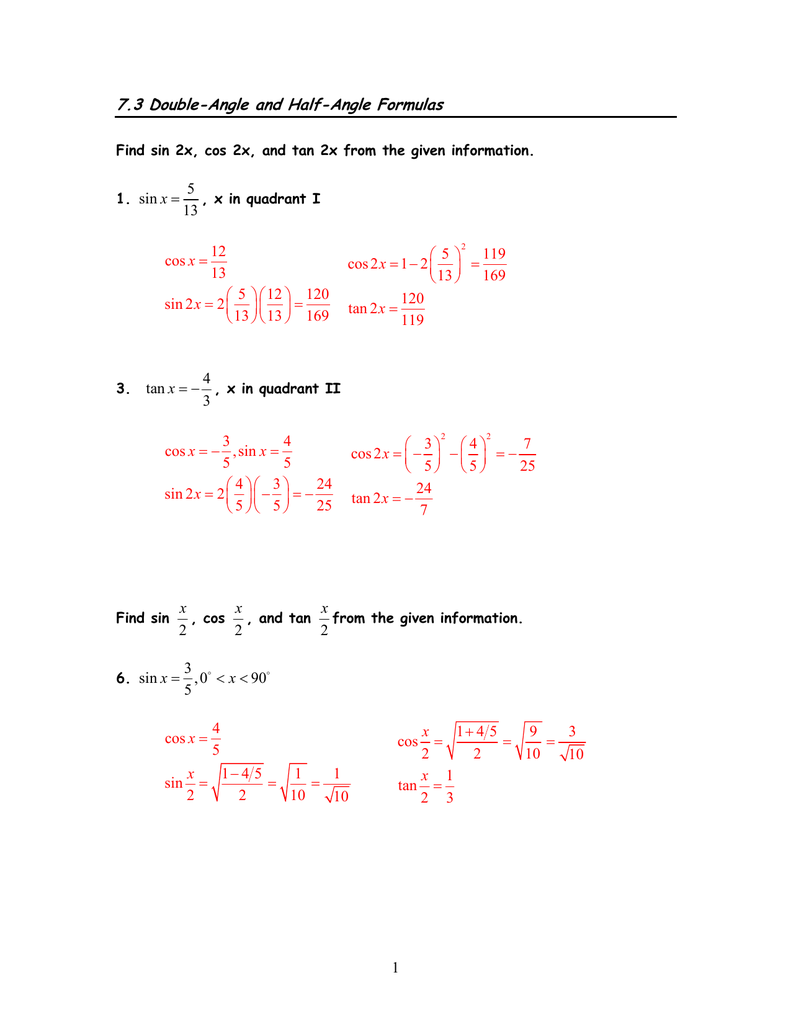
7 3 Double Angle And Half

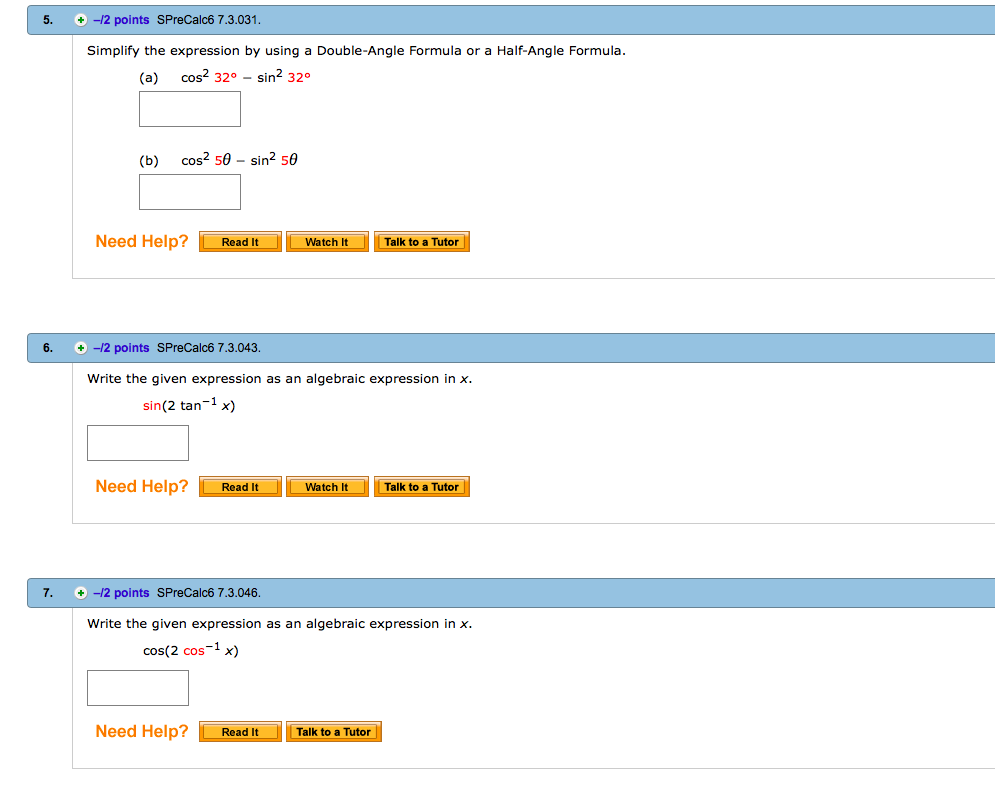
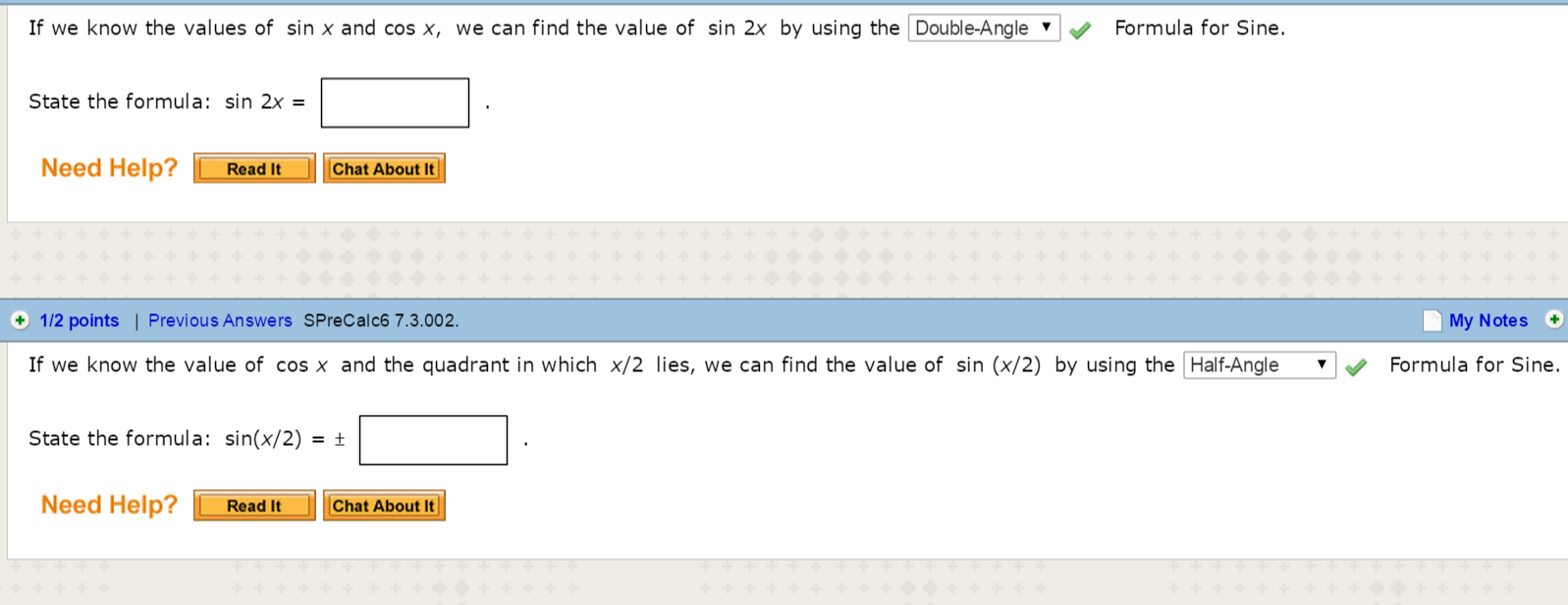
1 14 Points Sprecalc6 7 3 004 Find Sin 2x Cos 2x Chegg Com

1 Sin 2 X Formula Sepertikisahku

How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube

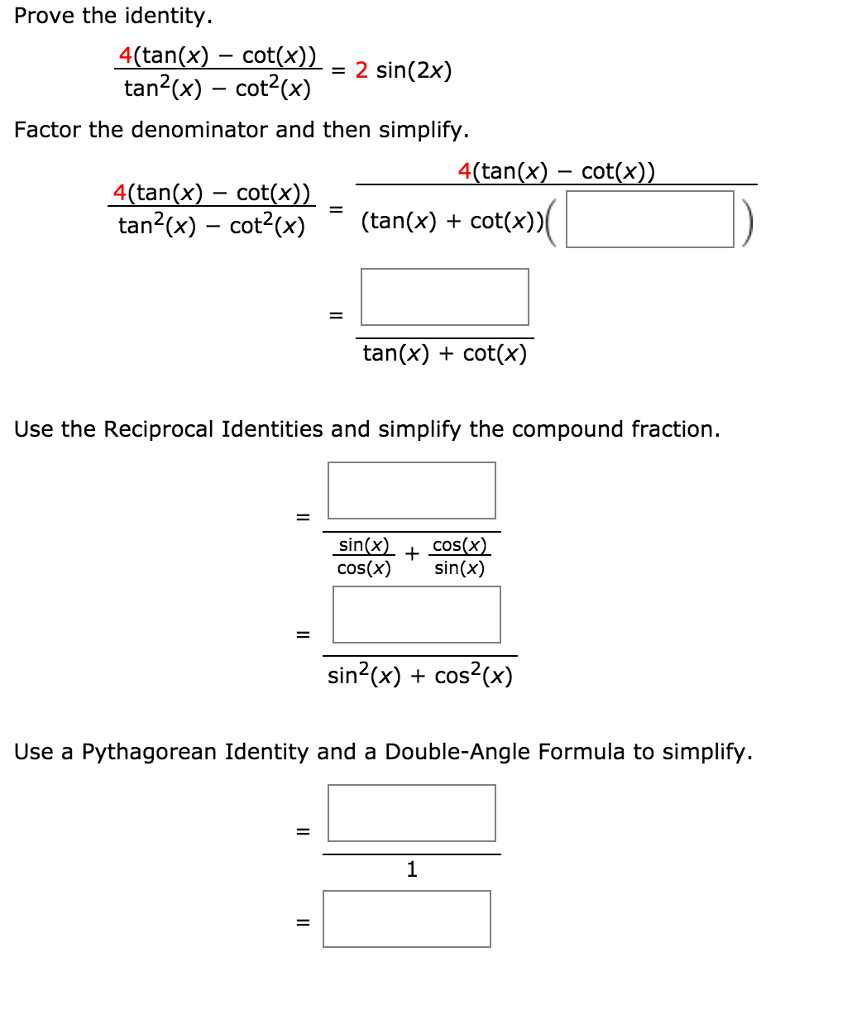
Prove The Identity 4 Tan X Cot X Tan 2 X Chegg Com

Trig Identity Sec2x Minus Tan2x T10 Youtube

Tan 2x Cot 2x 2

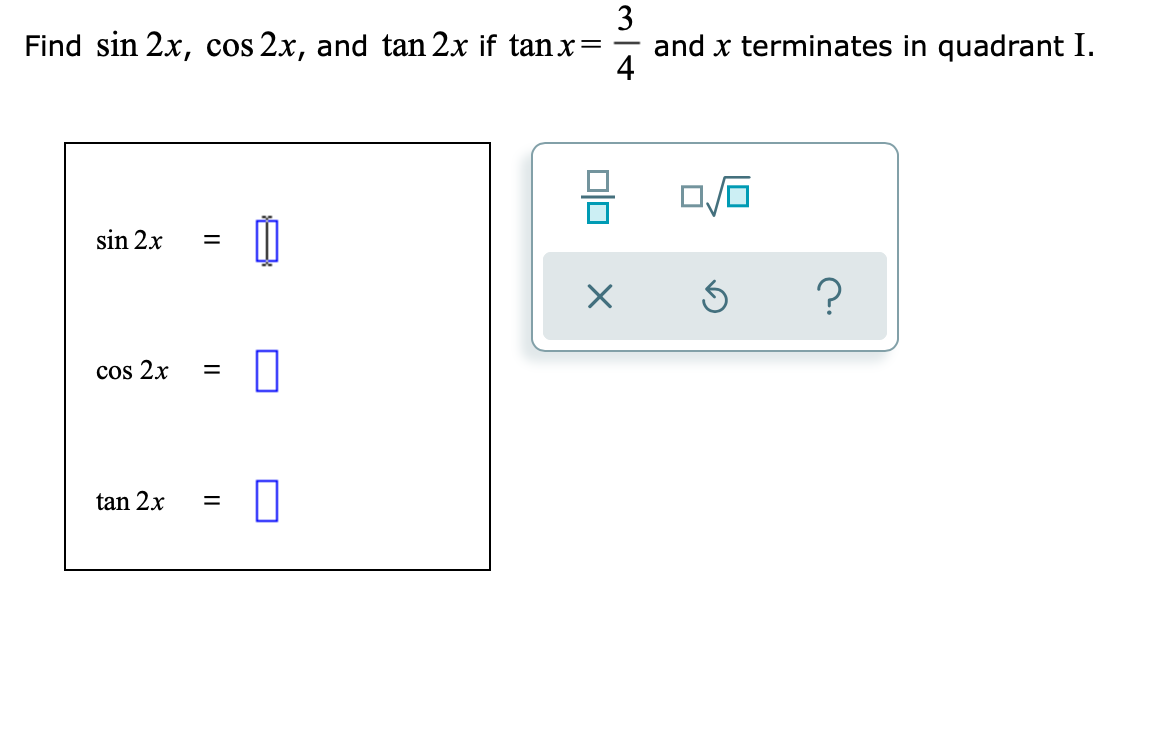
Answered 3 And X Terminates In Quadrant I 4 Bartleby